Classement ELO des écoles de commerce

Ce modèle est simple à comprendre et à mettre en œuvre et, sur cet exemple, il correspond à l’intuition : un bon outil de décision.

Cependant, il ne tient pas compte de deux phénomènes :

Pour prendre en compte ces deux phénomènes, on peut se tourner vers le classement ELO.

Le système ELO a été inventé dans les années 1960 pour classer des joueurs d’échecs, et a depuis acquis une solide légitimité. Utilisé par la fédération internationale d’échecs depuis environ 50 ans, il a été adapté et utilisé pour d’autres sports : go, football, e-sports.

Chaque joueur X se voit attribuer un score (notons le S_X). Les grands principes sont les suivants :

Le modèle ELO peut être utilisé comme un outil de prédiction. En effet, l’écart de score entre deux joueurs indique une probabilité de victoire.

Ici par exemple, les scores nous apprennent que le joueur B a environ 46% de chances de gagner son prochain match contre le joueur C.

Ceci provient de la formule de prédiction générale (1) donnée en annexe.

Différences entre SIGEM et ELO

Contrairement au modèle SIGEM, le modèle ELO tient compte :

• de l’ensemble des matchs disputés sur le tournoi
• pour chaque match : du niveau relatif des deux adversaires

Sur l’exemple précédent, les rangs SIGEM et ELO des trois joueurs sont identiques.

En modifiant les résultats, on peut obtenir des classements différents. Il suffit, par exemple, d’augmenter un peu le nombre de victoires de B contre A (qui est un très bon joueur)  et de resserrer le score entre B et C :

On retiendra que les modèles ELO et SIGEM peuvent diverger :

• lorsque les duels SIGEM sont serrés
• lorsque des joueurs faibles ont quelques victoires contre des joueurs forts

On pourrait se demander dans ce cas “quel est le vrai classement ?”. La réponse est bien sûr : aucun. Tout classement repose sur des hypothèses et met en avant certains phénomènes. La question doit plutôt être remplacée par : “quel classement met le plus l’accent sur les phénomènes que je souhaite prendre en compte ?”

Score ELO des écoles de commerce de 2017 à 2024

Le score ELO que nous proposons est calculé à partir des tableaux de désistements croisés du SIGEM publiés sur le site Major Prepa.

• des scores de l’année n-1
• du tableau de désistements croisés de l’année n.

selon un estimateur de type maximum de vraisemblance à modèle gaussien.

Plus de détails sur l’algorithme ici.

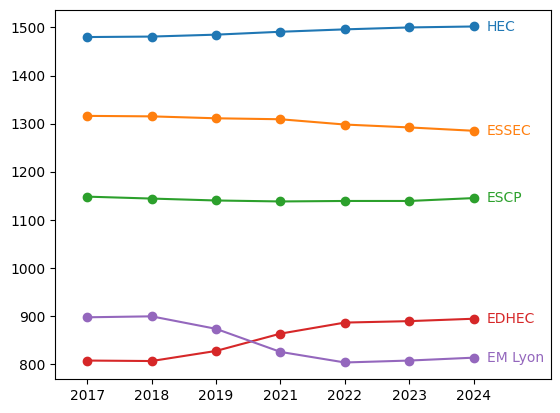
Voici les 24 grandes écoles classées selon leur score ELO 2024 :

Le classement ELO 2024 est proche du SIGEM 2024. On observe quelques différences en deuxième partie de tableau.

En particulier, les positions EM Strasbourg/INSEEC et SCBS/Brest BS sont inversées. Ceci n’est pas étonnant : les rangs SIGEM de ces écoles reposent sur des duels très serrés.

En appliquant la formule (1) à ces résultats, on constate par exemple que, selon notre modèle ELO, Audencia a environ 15% de chances de “prendre” un étudiant à SKEMA. Même écart pour EM Lyon / EDHEC.

Evolution du score ELO depuis 2017

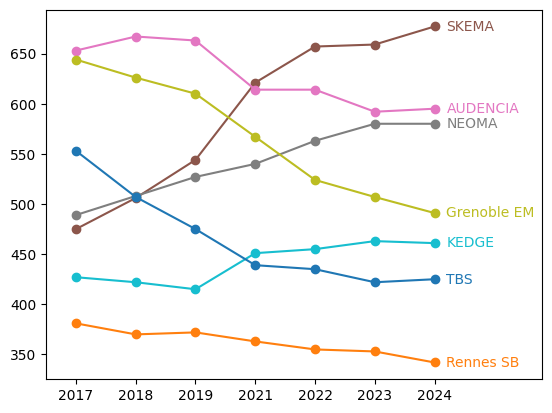
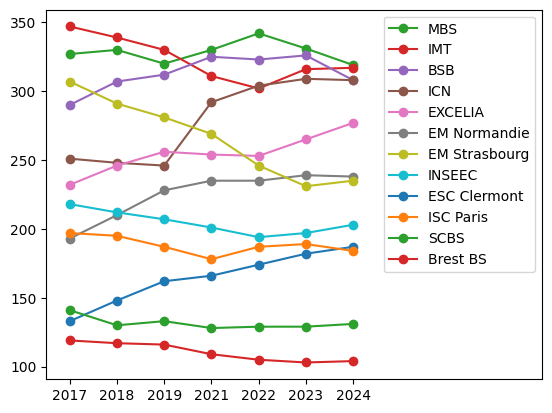
Pour plus de clarté, on sépare en trois graphiques : rangs 1-5, 6-12 et 13-24.

Comment améliorer le modèle

Toutes suggestions ou données complémentaires susceptibles d’améliorer le modèle sont les bienvenues : lionel.magnis At ac-lille.fr

Matchs multi-joueurs

Les données publiques présentent les désistements croisés sous la forme de matchs à 2 écoles. En réalité, la plupart des étudiants font leur choix parmi plusieurs écoles.

Par exemple, prenons le cas d’un étudiant admis à BSB, l’IMT, Excelia et l’INSEEC, et qui choisit d’aller à Excelia. Il s’agit donc d’un match à 4 écoles, remporté par Excelia.

Dans le tableau de désistements croisés, ceci donnera lieu à 3 victoires pour Excelia et 1 défaite pour chacune des trois autres écoles : 3 matchs au lieu d’1 seul.

Les calculs seraient plus fidèles à la réalité si on disposait des données concernant les multi-admis. Autrement dit, pour chaque groupe d’écoles possible, le nombre d’étudiants admis dans toutes les écoles du groupe et leur répartition finale.

A partir de ces données,  on pourrait adapter le modèle ELO pour traiter des matchs multi-joueurs.

Si quelqu’un dispose des données multi-admis et accepte de les partager, je l’en remercie chaleureusement.

Remplissage

Certaines écoles ne remplissent pas toutes les places ouvertes au concours. Pour ces écoles, le nombre d’étudiants intégrés est un indicateur d’attractivité. Par exemple, Brest BS a intégré 3 étudiants en 2023, et 11 étudiants en 2024.

Cette progression, qui semble indiquer une augmentation d’attractivité, n’apparaît pas dans le score ELO, car  10 de ces 11 étudiants ne rapportent pas de victoire contre une autre école : ils n’ont été admis qu’à Brest.

Toute suggestion sur la prise en compte de ce phénomène (et plus généralement : des étudiants admis à une seule école) est la bienvenue.

Annexe : algorithme de calcul du score ELO

On considère un tournoi à n joueurs. On souhaite évaluer leurs niveaux en fonction des résultats du tournoi, à l’aide d’un score.

Pour tous entiers i et j entre 1 et n, on note V_i,j le nombre de victoires du joueur i contre le joueur j lors du tournoi.

Pour tout i entre 1 et n, on note 𝜇_i le score du joueur i avant le tournoi et X_i son score après le tournoi.

Hypothèses :

• les scores 𝜇₁, 𝜇₂, …, 𝜇_n sont connus
• pour tout i, X_i est une variable aléatoire qui suit une loi normale d’espérance 𝜇_i et d'écart-type σ = 5
• pour tous entiers i et j, la probabilité que le joueur i batte le joueur j sur 1 match est :

• les résultats des matchs sont indépendants
• les variables aléatoires X₁, …, X_n sont indépendantes

(L'écart-type 5 est un choix arbitraire. Concrètement, ceci signifie que les scores avant/après tournoi diffèrent de quelques points. On pourrait choisir une autre valeur, voire même des écarts-types différents pour les différents joueurs.)

L’idée est de trouver des réels x₁, …, x_n qui maximisent la probabilité P(X₁=x₁, …, X_n=x_n) conditionnelle au résultat du tournoi.

(en toute rigueur, X₁=x₁ signifie plutôt ici x₁-h ≤ X₁ ≤ x₁+h avec h petit).

En appliquant la formule de Bayes, ceci revient à maximiser la fonction :

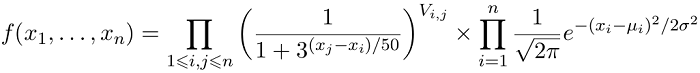
Ceci est encore équivalent (et c’est plus pratique) à minimiser la fonction :

Remarque 1 : pour l’année d’initialisation, pas de modèle d’évolution : on enlève ce terme.

Remarque 2 : ce terme est constant, il ne change rien à la minimisation.

Pour la minimisation, on a utilisé la méthode BFGS disponible via la commande scipy.optimize.minimize de Python.